viernes, 7 de junio de 2013
tipos de funciones Lizbeth Huesca Castillo
Las funciones se pueden representar de distintas maneras: • Como expresión matemática: ecuaciones de la forma y = f(x), que permiten representar el comportamiento de la función a lo largo de todo su dominio. Ejemplo: y=x+2.
• Como pares ordenados: pares ordenados, muy usados en teoría de grafos. Ejemplo: A={(-2, 0),(-1, 1),(0, 2),(1, 3), ... (x, x+2)}
• Como proposición: una descripción por comprensión de lo que hace la función. Ejemplo: "Para todo x, número entero, y vale x más dos unidades".
• Como tabulación: tabla que permite representar algunos valores discretos de la función.
x -2 -1 0 1 2 3
y 0 1 2 3 4 5
Clasificación de funcionesLas funciones se clasifican en algebraicas y trascendentes.En las funciones algebraicas las operaciones que hay que efectuar con la variable independiente son: la adición, sustracción, multiplicación, división, potenciación y radicación.
Las funciones algebraicas pueden ser: explícitas e implícitas. Son explícitas cuando se pueden obtener las imágenes de x por simple sustitución.
Ejemplo: f(x) = 5x – 2.
Y serán implícitas si no se pueden obtener las imágenes de x por simple sustitución, sino que es preciso efectuar operaciones. 5x - y - 2 = 0. En este caso hay que despejar primero la variable y.
A- Funciones Algebraicas
Las funciones algebraicas se clasifican en polinómicas, racionales y radicales a trozos.
1-Funciones polinómicas: Son las funciones que vienen definidas por un polinomio.
f(x) = a0 + a1 x + a1 x² + a1 x³ +••• + an xn . Su dominio todo los números reales , es decir, cualquier número real tiene imagen.
Funciones polinomiales especiales:
Funciones polinómica de primer grado f(x) = mx +n con m ≠ 0. Donde m es la pendiente y b la ordenada en el origen, el dominio son todod lo numeros reales.Su gráfica es una recta oblicua, que queda definida por dos puntos de la función.
Ejemplo:
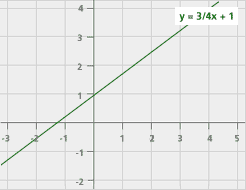
Funciones constantes: El criterio viene dado por un número real. f(x)= k. Es una función cuyo rango consta de un sólo número real.
La gráfica es una recta horizontal paralela a al eje de abscisas.
• Como pares ordenados: pares ordenados, muy usados en teoría de grafos. Ejemplo: A={(-2, 0),(-1, 1),(0, 2),(1, 3), ... (x, x+2)}
• Como proposición: una descripción por comprensión de lo que hace la función. Ejemplo: "Para todo x, número entero, y vale x más dos unidades".
• Como tabulación: tabla que permite representar algunos valores discretos de la función.
x -2 -1 0 1 2 3
y 0 1 2 3 4 5
Clasificación de funcionesLas funciones se clasifican en algebraicas y trascendentes.En las funciones algebraicas las operaciones que hay que efectuar con la variable independiente son: la adición, sustracción, multiplicación, división, potenciación y radicación.
Las funciones algebraicas pueden ser: explícitas e implícitas. Son explícitas cuando se pueden obtener las imágenes de x por simple sustitución.
Ejemplo: f(x) = 5x – 2.
Y serán implícitas si no se pueden obtener las imágenes de x por simple sustitución, sino que es preciso efectuar operaciones. 5x - y - 2 = 0. En este caso hay que despejar primero la variable y.
A- Funciones Algebraicas
Las funciones algebraicas se clasifican en polinómicas, racionales y radicales a trozos.
1-Funciones polinómicas: Son las funciones que vienen definidas por un polinomio.
f(x) = a0 + a1 x + a1 x² + a1 x³ +••• + an xn . Su dominio todo los números reales , es decir, cualquier número real tiene imagen.
Funciones polinomiales especiales:
Funciones polinómica de primer grado f(x) = mx +n con m ≠ 0. Donde m es la pendiente y b la ordenada en el origen, el dominio son todod lo numeros reales.Su gráfica es una recta oblicua, que queda definida por dos puntos de la función.
Ejemplo:

Funciones constantes: El criterio viene dado por un número real. f(x)= k. Es una función cuyo rango consta de un sólo número real.
La gráfica es una recta horizontal paralela a al eje de abscisas.

Función identica: Es una función definida por f(x) = x, es decir el dominio de la función es igual al rango dela función. Su gráfica es una línea recta que pasa por el origen

2-Funciones racionales : Es una función definida mediante el cociente de dos funciones polinomiales
El dominio lo forman todos los números reales excepto los valores de x que anulan el denominador.
-Funciones trascendentes
La variable independiente figura como exponente, o como índice de la raíz, o se halla afectada del signo logaritmo o de cualquiera de los signos que emplea la trigonometría.
Abraham Munive Gonzales
NO: 34
NO: 34
Función polinomial
Una empresa produce placas de acero de 50 cm por 70 cm si a cada placa se le restan “x” cantidad del lado mas corto y “2x” del lado mas largo
Una empresa produce placas de acero de 50 cm por 70 cm si a cada placa se le restan “x” cantidad del lado mas corto y “2x” del lado mas largo
¿Cómo se expresa en una función polinomial?
f(x)= (50-x)(70-2x)
f(x)=x²-120x+3500
f(x)= (50-x)(70-2x)
f(x)=x²-120x+3500
¿Cuanto queda de area si se le quitan 5 cm?
Para simplificar el trabajo se utiliza el
polinomio original f(x)= (50-x)(70-2x)
f(5)= (50-(5))(70-2(5))
f(5)=(45)(60)
f(5)= 2700
f(5)= (50-(5))(70-2(5))
f(5)=(45)(60)
f(5)= 2700
Función racional
hicieron el conteo de todas las personas en una colonia de 676 metros cuadrados y dio como resultado 1342
¿como expresarlo en una función simple para detectar?
hicieron el conteo de todas las personas en una colonia de 676 metros cuadrados y dio como resultado 1342
¿como expresarlo en una función simple para detectar?
F(X)=676x²/1342x
¿Cómo se obtendría cuantas personas hay en 2
metros cuadrados?
F(X)=676x²/1342x
F(2)=676(2)²/1342(2)
F(2)=2704/2684
F(2)=1
F(2)=676(2)²/1342(2)
F(2)=2704/2684
F(2)=1
Mendoza Vázquez Antonio Raymundo 4°D N°31
Gráficas de las funciones
Hay que ser honestos, cuando uno gráfica una función, a simple vista, sabemos de que tipo de función se tratará, y podremos darnos cuenta a la hora de ir dando valores a la x de la función, el sentido que tomará la dichosa gráfica, las importantes funciones de Pre-cálculo son:
Función Inversa
Función Valor Absoluto
Gráficas de las funciones
Hay que ser honestos, cuando uno gráfica una función, a simple vista, sabemos de que tipo de función se tratará, y podremos darnos cuenta a la hora de ir dando valores a la x de la función, el sentido que tomará la dichosa gráfica, las importantes funciones de Pre-cálculo son:
Función Inversa
Función Escalonada
Función de Identidad
Función Constante
Función Polinomial
Función Cúbica
Función cuadrática
Función Racional
Función Exponencial
Función Logarítmica
Funciones Trigonométricas
Función Circular
Mendoza Vázquez Antonio Raymundo 4°D N°31
Problema de Función Polinomial
Juan fue nombrado administrador de una página de facebook.
La función F(x)=x4+4x3-12x2-32x+64 modela el número de personas a las que las publicaciones de la página, llegaron. Ten en cuenta que la unidad de x es un mes. x=1=1mes
Encuentra
a) ¿A cuántas personas habían llegado las publicaciones cuando Juan fue nombrado administrador?
Respuesta
F(0)=(0)4+4(0)3-12(0)2-32(0)+64=64
A 64 personas habían llegado las publicaciones cuando Juan fue nombrado administador
b) ¿A cuántas personas llegó en su primer mes de gestión?
Respuesta
F(1)=(1)4+4(1)3-12(1)2-32(1)+64=1+4-12-32+64=25
Llego a 25 personas en su primer mes de gestión
c) ¿En qué mes se le cayó la página, llegando a ninguna persona?
Respuesta: Buscaremos, por medio de la división sintética, el cero real
Ahora procedemos a realizar
F(2)=(2)4+4(2)3-12(2)2-32(2)+64=16+32-48-64+64=0
La página se le cayó en el segundo mes, llegando a ninguna persona
d) ¿A cuántas personas llegó en 1 año? 1 año=12 meses
F(12)=(12)4+4(12)3-12(12)2-32(12)+64=20736+6912-1728-384+64=25600
Al año de ser administrador, las publicaciones en la página llegaran a 25600 personas
Gráfica
Función Racional
Don Pepe decidió reabrir su dulcería
La función F(x)=4x-1/x+1 modela los ingresos y pérdidas que tuvo durante las primeras semanas.
F en miles, 1 unidad= 1000 pesos
F(x)=4x-1/x+1
donde
n=1 y m=1, por lo tanto si hay asíntota horizontal, que será de 4, ya que y=a/b=4/1
y su asíntota vertical será de -1, ya que x+1=0 por lo tanto x=-1
y así trazaremos la gráfica con las asíntotas
Responde:
a) Para reabrir la dulcería, ¿cuánto tuvo que gastar don Pepe?
Respuesta: Modelamos la función con 0, que es el valor de cuando don Pepe reabrió la dulcería
F(0)=4(0)-1/(0)+1=-1
Para reabrir su dulcería, Don Pepe tuvo que gastar 1000 pesos
b) ¿Y en la primera semana, tuvo ingresos o pérdidas, y de cuánto fueron?
Respuesta: Para esto, haremos la función de 1, que es el número de semanas
F(1)=4(1)-1/(1)+1=1.5(1000)=1500
Don Pepe obtuvo un ingreso de 1500 pesos, en la primera semana después de reabrir su dulcería
c) ¿Porque crees que en F(0) el resultado fue negativo y en F(1) fue positivo)
Porque para reabrir su tienda, Don Pepe tuvo que invertir 1000 pesos, pero a la primera semana después de reabrir la dulcería, Don Pepe tuvo de ganancia 1500 pesos, con los que recupero su inversión.
d) ¿Cuánto ganó Don Pepe en la décima semana?
Modelamos F(10)
F(10)=4(10)-1/(10)+1=39/11=3.545454...(1000)=3545.45
En la décima semana, Don Pepe ganará 3545.45 pesos de ingresos
e)¿Y en medio año?
Un año tiene 52 semanas, por lo tanto medio año tiene 26 semanas
F(26)=4(26)-1/(26)+1=103/27=3.814814...(1000)=3814.81
En medio año, Don Pepe obtendrá 3814.81 pesos de ingresos
También podemos deducir que, quizá tener una dulcería podría ser buen negocio
f) ¿Tienen límite los ingresos de Don Pepe?
Si, los ingresos de Don Pepe tendrán un límite y será hasta cerca de los 4 mil pesos, eso podemos demostrarlo dividiendo 4x-1/x+1, donde el cociente será de 4 y el residuo de -5
Gráfica
Problema de Función Polinomial
Juan fue nombrado administrador de una página de facebook.
La función F(x)=x4+4x3-12x2-32x+64 modela el número de personas a las que las publicaciones de la página, llegaron. Ten en cuenta que la unidad de x es un mes. x=1=1mes
Encuentra
a) ¿A cuántas personas habían llegado las publicaciones cuando Juan fue nombrado administrador?
Respuesta
F(0)=(0)4+4(0)3-12(0)2-32(0)+64=64
A 64 personas habían llegado las publicaciones cuando Juan fue nombrado administador
b) ¿A cuántas personas llegó en su primer mes de gestión?
Respuesta
F(1)=(1)4+4(1)3-12(1)2-32(1)+64=1+4-12-32+64=25
Llego a 25 personas en su primer mes de gestión
c) ¿En qué mes se le cayó la página, llegando a ninguna persona?
Respuesta: Buscaremos, por medio de la división sintética, el cero real
Ahora procedemos a realizar
F(2)=(2)4+4(2)3-12(2)2-32(2)+64=16+32-48-64+64=0
La página se le cayó en el segundo mes, llegando a ninguna persona
d) ¿A cuántas personas llegó en 1 año? 1 año=12 meses
F(12)=(12)4+4(12)3-12(12)2-32(12)+64=20736+6912-1728-384+64=25600
Al año de ser administrador, las publicaciones en la página llegaran a 25600 personas
Gráfica
Función Racional
Don Pepe decidió reabrir su dulcería
La función F(x)=4x-1/x+1 modela los ingresos y pérdidas que tuvo durante las primeras semanas.
F en miles, 1 unidad= 1000 pesos
F(x)=4x-1/x+1
donde
n=1 y m=1, por lo tanto si hay asíntota horizontal, que será de 4, ya que y=a/b=4/1
y su asíntota vertical será de -1, ya que x+1=0 por lo tanto x=-1
y así trazaremos la gráfica con las asíntotas
Responde:
a) Para reabrir la dulcería, ¿cuánto tuvo que gastar don Pepe?
Respuesta: Modelamos la función con 0, que es el valor de cuando don Pepe reabrió la dulcería
F(0)=4(0)-1/(0)+1=-1
Para reabrir su dulcería, Don Pepe tuvo que gastar 1000 pesos
b) ¿Y en la primera semana, tuvo ingresos o pérdidas, y de cuánto fueron?
Respuesta: Para esto, haremos la función de 1, que es el número de semanas
F(1)=4(1)-1/(1)+1=1.5(1000)=1500
Don Pepe obtuvo un ingreso de 1500 pesos, en la primera semana después de reabrir su dulcería
c) ¿Porque crees que en F(0) el resultado fue negativo y en F(1) fue positivo)
Porque para reabrir su tienda, Don Pepe tuvo que invertir 1000 pesos, pero a la primera semana después de reabrir la dulcería, Don Pepe tuvo de ganancia 1500 pesos, con los que recupero su inversión.
d) ¿Cuánto ganó Don Pepe en la décima semana?
Modelamos F(10)
F(10)=4(10)-1/(10)+1=39/11=3.545454...(1000)=3545.45
En la décima semana, Don Pepe ganará 3545.45 pesos de ingresos
e)¿Y en medio año?
Un año tiene 52 semanas, por lo tanto medio año tiene 26 semanas
F(26)=4(26)-1/(26)+1=103/27=3.814814...(1000)=3814.81
En medio año, Don Pepe obtendrá 3814.81 pesos de ingresos
También podemos deducir que, quizá tener una dulcería podría ser buen negocio
f) ¿Tienen límite los ingresos de Don Pepe?
Si, los ingresos de Don Pepe tendrán un límite y será hasta cerca de los 4 mil pesos, eso podemos demostrarlo dividiendo 4x-1/x+1, donde el cociente será de 4 y el residuo de -5
Gráfica
Problema. 9.
Sea t el tiempo en segundos y d(t) “la distancia en metros que una piedra cae después de
t segundos”. La frase “la distancia que cae la piedra después de t segundos es 5t2
metros” se puede escribir como d(t) = 5t2
. Por ejemplo,
d(1) = 5(1)2
= 5
significa “la distancia que la piedra cae después de 1 segundo es 5 metros”
d(4) = 5(4)2
= 80
significa “la distancia que la piedra cae después de 4 segundos es 80 metros”
Problema. 10.
Encuentre el valor de la función f(x) = 2x2
– 4x + 1, cuando x = -1, x = 0, y, x = 2.
Solución.
Cuando x = -1, el valor de f está dado por
f(-1) = 2(-1)2
– 4(-1) + 1 = 2 + 4 + 1 = 7
Cuando x = 0, el valor de f está dado por
f(0) = 2(0)2
– 4(0) + 1 = 1
Cuando x = 2, el valor de f está dado por
f(2) = 2(2)2
– 4(2) + 1= 8 -8 + 1 = 1
Con los datos de la izquierda se
puede construir la siguiente tabla:
x f(x)
-1 7
0 1
2 1
JANETH CITALAN RODRIGUEZ
Sea t el tiempo en segundos y d(t) “la distancia en metros que una piedra cae después de
t segundos”. La frase “la distancia que cae la piedra después de t segundos es 5t2
metros” se puede escribir como d(t) = 5t2
. Por ejemplo,
d(1) = 5(1)2
= 5
significa “la distancia que la piedra cae después de 1 segundo es 5 metros”
d(4) = 5(4)2
= 80
significa “la distancia que la piedra cae después de 4 segundos es 80 metros”
Problema. 10.
Encuentre el valor de la función f(x) = 2x2
– 4x + 1, cuando x = -1, x = 0, y, x = 2.
Solución.
Cuando x = -1, el valor de f está dado por
f(-1) = 2(-1)2
– 4(-1) + 1 = 2 + 4 + 1 = 7
Cuando x = 0, el valor de f está dado por
f(0) = 2(0)2
– 4(0) + 1 = 1
Cuando x = 2, el valor de f está dado por
f(2) = 2(2)2
– 4(2) + 1= 8 -8 + 1 = 1
Con los datos de la izquierda se
puede construir la siguiente tabla:
x f(x)
-1 7
0 1
2 1
JANETH CITALAN RODRIGUEZ
Salvador García Domínguez No. 19
2
( ) = +
x
f x
es la regla que toma un número, lo divide por 2 y luego le suma 7 al cociente. Si se da
un valor para x, ese valor se sustituye en x en la fórmula, y la ecuación se resuelve para
f(x), entonces estamos evaluando la función en un valor de su dominio. Por ejemplo, si
x = 4,
4
(4) 7 9 2
f =+=
Si x = 6, 6
(6) 7 10 2
f =+=
Problema. 7.
Si f(x) = x2
+ x -2. Calcular f(-x) y –f(x).
f(-x) = (-x)
2
+ (-x) -2 = x2
- x -2
En este caso f (-x) no es lo mismo que –f(x), porque –f(x) es el número negativo de f(x),
es decir
-f(x) = -(x2
+ x -2) = -x2
- x +2
Areli Rodriguez Macias
( ) = +
x
f x
es la regla que toma un número, lo divide por 2 y luego le suma 7 al cociente. Si se da
un valor para x, ese valor se sustituye en x en la fórmula, y la ecuación se resuelve para
f(x), entonces estamos evaluando la función en un valor de su dominio. Por ejemplo, si
x = 4,
4
(4) 7 9 2
f =+=
Si x = 6, 6
(6) 7 10 2
f =+=
Problema. 7.
Si f(x) = x2
+ x -2. Calcular f(-x) y –f(x).
f(-x) = (-x)
2
+ (-x) -2 = x2
- x -2
En este caso f (-x) no es lo mismo que –f(x), porque –f(x) es el número negativo de f(x),
es decir
-f(x) = -(x2
+ x -2) = -x2
- x +2
Areli Rodriguez Macias
Suscribirse a:
Comentarios
(Atom)




















